Sistem bilangan BCD dan BCH

بسم الله الرحمن الرحيم

اللهم صل على سيدنا محمد واله وصحبه وسلم

Materi Sistem Komputer Kelas X  Sistem bilangan Binary Code Decimal (BCD) dan Binary Code Hexadecimal (BCH)

I. Binary Coded Decimal (BCD)
Dalam system komputer dan sistem elektronik, Binary Coded Decimal (BCD) adalah kelas dari pengkodean biner dari angka desimal di mana setiap digit desimal diwakili oleh sejumlah bit yang tetap, biasanya empat atau delapan. pola bit ini biasanya digunakan untuk tanda atau indikasi lain (misalnya, kesalahan atau overflow).
kebajikan utama BCD adalah representasi yang lebih akurat dan pembulatan dari jumlah desimal serta kemudahan konversi menjadi representasi yang terbaca oleh manusia, dibandingkan dengan sistem posisional biner. kelemahan utama BCD adalah peningkatan kecil dalam kompleksitas sirkuit yang diperlukan untuk melaksanakan aritmatika dasar dan penyimpanan sedikit kurang padat.
Pada system bilangan BCD metodenya mirip dengan bilangan biner biasa; hanya saja dalam proses konversi, setiap digit dari bilangan desimal dikonversi satu per satu, bukan secara keseluruhan seperti konversi bilangan desimal ke biner biasa. Hal ini lebih bertujuan untuk “menyeimbangkan” antara kurang fasihnya manusia pada umumnya untuk melakukan proses konversi dari desimal ke biner -dan- keterbatasan komputer yang hanya bisa mengolah bilangan biner. Perhatikan ulasan berikut ini

Contoh 1 :
Berapa nilai BCD dari bilangan  487 (10)
   4       8       7          Desimal
0100 1000 0111       Biner Code Desimal
Dalam contoh ini BCD terdiri dari 3 kelompok bilangan masing-masing terdiri dari 4 bit , dan jika bilangan desimal tersebut di atas dikonversi ke dalam bilangan biner secara langsung adalah 487(10) = 111100111(bcd)dan hanya memerlukan 9 bit. Untuk contoh proses sebaliknya dapat dilihat di bawah ini.

Contoh 2:
Biner Code Desimal          0111  0001  0010  0001
Desimal                                7       1         2        1
Jadi bentuk BCD di atas adalah bilangan X(10) = 7121.

Tetapi, berhubung hasil yang diinginkan adalah bilangan BCD, maka basis bilangannya tinggal ditulis sebagai berikut :

Contoh 3 :
210—-> 0010BCD
810—-> 1000BCD
910—-> 1001BCD
maka, nilai BCD dari 289 adalah 0010 1000 1001BCD.

Perlu diingat bahwa setiap digit pada bilangan desimal dikonversi menjadi 4 bit bilangan BCD.

Contoh 4 :
misalkan bilangan yang ingin dikonversi adalah 38010.
310—–> 0011BCD
810 —–> 1000BCD
010—–> 0000BCD
maka, nilai BCD dari 30910 adalah 0011 1000 0000BCD.

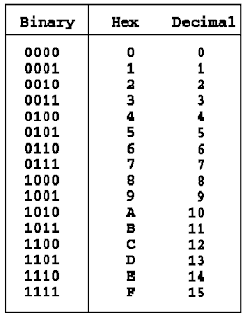
Agar lebih mudah dalam pengkonversian gunakan table konversi di bawah ini

II. Binary Code Hexadecimal (BCH)
Pada Bilangan Hexadecimal setiap tempat dapat terdiri dari 16 karakteryang berbeda-beda, baik angka maupun huruf. Bentuk biner untuk 16 elemen memerlukan 4 bit. Sebuah BCH mempunyai 4 bit biner untuk setiap tempat bilangan heksadesimal.

Contoh :

Z(16) = 21AF
Bilangan Heksadesimal       2       3         A       F
Biner Code Heksadesimal   0010  0011  1010  1111
Untuk proses sebaliknya, setiap 4 bit dikonversi ke dalam bilangan heksadesimal.

Contoh :
Biner Code Heksadesimal   1111 0100 0010 1000
Bilangan Heksadesimal          F      4       2        8
Jadi bentuk BCH diatas adalah bilangan Z(16) = F428.


Semoga Bermanfaat, Untuk Materi Lengkap Mata Pelajaran Sistem Komputer silahkan simak di sini